Elliptische Planetenbahn
Im Folgenden finden sie eine Beispielrechnung zur Berechnung der Venusposition.
Das zugrunde liegende physikalische Problem ist das Zweikörperproblem: Zwei punktförmige
Massen (Sonne und Venus) die aufeinander Kräfte (Gravitation) ausüben.
In der Astronomie wird das Zweikörperproblem auch als Keplerproblem bezeichnet.
Durch die Lösung der Keplergleichung kann man dann die Planetenpositionen berechnen.
Bei der Lösung der Keplergleichung vernachlässigt man die Gravitationskräfte der
Planeten untereinander. Deshalb ist die Genauigkeit der berechneten Planetenpositionen
auch beschränkt.
Ich versuche in der nachfolgenden Beispielrechnung alle notwendingen Formel zusammen zu tragen.
Eine Herleitung der Formeln werden sie allerdings nicht immer finden. Dazu verweise ich auf
die restlichen Kapitel bzw. auf die gängige Literatur zu diesem Thema.
In die einzelnen Kapitel eingebettet finden sie jeweils kleine Javascript-Snippets mit Hilfe
derer sie die Berechnung Online nachvollziehen können. Die Snippets bauen aufeinander auf.
Sie sollten sie also sequentiell ausführen. Das letzte Snippet zeichnet dann noch eine Sternkarte mit der
berechneten Position.
Die Javascript-Snippets beruhen auf einer kleiner Astronomie Bibliothek, welche sie
auch als ZIP-Archiv herunterladen können. Siehe Abschnitt
Downloads
.
Julianisches Datum
In der Astronomie ist das
Julianische Datum
zur Zeitrechnung sehr beliebt.
Das
Julianische Datum
ist definiert als die Zahl der Tage, welche seit dem
1. Januar 4713 v. Chr. 12:00 vergangen sind. In
Das Julianische Datum
finden sie eine Herleitung
der Berechnungsformel.
Berechnungsformeln
- Man berechnet zuerst das
Julianische Datum
\(\mbox{JD}_0\)am 1.1 12 Uhr UT eines Jahrs:
| $$\begin{eqnarray*}
\mathrm{JD}_0(y)&=& \mbox{int}(365.25(4712 + y)+0.75) + B \\
\mathrm{B}(y)&=&\left\{
\begin{array}{ll}
0 \\
\mbox{Julianisches Datum, bis einschließlich 4.10.1582} \\
\\
-\mbox{int}(y/100)+\mbox{int}(y/400) +2 \\
\mbox{Gregorianisches Datum}
\end{array}\right.
\end{eqnarray*}$$ |
|
- Daraus kann man dann das
Julianische Datum
\(\mbox{JD}\)zu einem bliebigen Zeitpunkt ermitteln:
| $$
\mathrm{JD}(d,m,y,UT)=
\left\{
\begin{array}{l}
\mathrm{JD}_0(y)+\mbox{Days}(m-1)+d-1+(UT-12)/24 \\
\mbox{Datum bis zum 28. Februar} \\
\\
\mathrm{JD}_0(y+1)-365+\mbox{Days}(m-1)+d-1+(UT-12)/24 \\
\mbox{Datum nach dem 28. Februar}.
\end{array}
\right.
$$ |
| Symbol
| Bedeutung
|
|---|
| \(d\) | Tag
|
| \(m\) | Monat
|
| \(y\) | Jahr
|
| \(UT\) | Weltzeit, gemessen von 0..24h
|
| \(\mbox{days}(m)\) | Zahl der Tage eines Monats,
\(\mbox{days}(1)=31\),
\(\mbox{days}(2)=28\)usw.
|
| \(\mbox{Days}(m) = \sum_{n=1}^{m} \mbox{days}(n)\) | Insgesamt vergangene Tage
|
| \(\mbox{JD}\) | Julianisches Datum zu einem beliebigen Zeitpunkt
|
| \(\mbox{JD}_0\) | Julianisches Datum um 12 Uhr UT am 1.1 eines beliebigen Jahrs
|
Berechnung des julianischen Datums
Hier finden ein Snippet zur Berechung des
Julianische Datums
zum aktuellen Datum:
// get current date
var now = calc.currentDate();
print("year :",now.year);
print("month :",now.month);
print("day :",now.day);
print("hour :",now.hour);
print("minute :",now.minute);
// calculate julian date
global.julianDate = calc.julianDate(now.day, now.month, now.year, now.hour + now.minute / 60.0);
print("julian date :", global.julianDate);
Die Bibliothek
astro.calc.js
stellt die entsprechenden Funktionen bereit.
Die Implementierung ist nicht schwierig:
calc.julianDate = function (day, month, year, ut) {
var jd = null;
if (month <= 2) {
jd = calc.jd0(day, month, year);
} else {
jd = calc.jd0(day, month, year + 1) - 365;
}
jd += calc.daysUpToMonth(month) + day - 1;
if (calc.isGregorian(day, month, year))
jd += -10;
jd += (ut - 12) / 24.0;
return jd;
};
calc.jd0 = function (day, month, year) {
var result = math.int((4712 + year) * 365.25 + 0.75);
if (calc.isGregorian(day, month, year)) {
result += calc.LEAPDAYDELTA - math.int(year / 100) + math.int(year / 400);
}
return result;
};
Planet: Bahnelemente
Bahnelemente sind Parameter mit Hilfe derer eine Planetenbahn vollständig beschrieben wird.
Kennt man die Bahnelemente, dann kann man für jeden beliebiegen Zeitpunkt die Planetenposition
berechnen. In Abschitt
Bahnelemente
finden sie eine Beschreibung der Bahnelemente.
Bahnelemente nach JPL
Wir benutzen für unsere Rechnung die Bahnelemente, die vom Jet Propulsion Laboratory (JPL)
zur Verfügung gestellt werden.
Das JPL stellt auf seiner Webpräsenz
Bahnelemente
für die Planeten bereit.
Das JPL benutzt die Bahnelemente
\(a, e, i, L, \tilde{\omega}\)und
\(\Omega\). Dabei wird die mittlere Länge
gemäß der Formel
berechnet. Hier ist
\(T\)definiert als die Zahl der Jahrhunderte nache dem 1.1.2000:
| $$
T=\frac{t-2451545}{36525}
$$ |
Also hat man wie in Abschnitt
Bahnelemente
festgestellt 7 Bahnelemente (
\(a\),
\(e\),
\(i\),
\(\tilde{\omega}\),
\(\Omega\),
\(L_0\)und
\(\dot{L}\)).
| Symbol
| Bedeutung
|
|---|
| \(L\) | Mittlere Länge
|
| \(T\) | Zahl der Jahrhundert nach dem 1.1.2000
|
| \(t\) | Julianisches Datum
|
Beim Studium des verlinkten JPL-Dokuments werden sie feststellen, daß für die restlichen Bahnelemente eine ähnliche
Berechnungformel gilt. Also z.B für die große Halbachse
| $$\begin{equation}
a=a_0 + \dot{a} \frac{t-2451545}{36525}
\end{equation}$$ | (20) |
(2451545 is das Julianische Datum für den 1.1.2000).
Gibt es also mehr als sieben Bahnelemente? Wenn Sie das Zweikörperproblem lösen sind tatsächlich nur sieben Bahnelemente notwendig.
Im Sonnensysten wechselwirken aber alle Planeten miteinander. Beim Problem der Planetenpositionsberechnung handelt es sich also
nur näherungsweise um ein Zweikörperproblem. Die Abweichungen vom Zweikörperproblem kann man (ebenfalls näherungsweise) durch lineare Korrekturterme in den
Bahnelementen behandeln. Sie werden aber feststellen, daß die linearen Korrekturterme
(z.B.
\(\dot{a}_{\textrm{earth}}=0.00000562 \text{AE}/\textrm{Jahrhundert}\))
für die Bahnelemente eher klein sind.
Die Zahlenwerte für die mittlere Länge der Erde
\(L_0\)und
\(\dot{L}\)kann man auch sehr gut anschaulich verstehen:
Die Umlaufgeschwindigkeit der Erde um die Sonne ist
| $$\begin{equation}
\dot{L} \approx \frac{360 \textrm{Grad}}{\textrm{Jahr}} = \frac{360 \cdot 100 \thinspace \textrm{Grad}}{\textrm{Jahrhundert}} = 36000 \frac{\textrm{Grad}}{\textrm{Jahrhundert}}
\end{equation}$$ | (21) |
Was noch fehlt ist die mittlere Länge
\(L_0\)am 1.1.2000, welche ungefähr 100 Grad betrug. Diese Behauptung können
Sie auch leicht verifizieren: Am 21.3.2000 (Sonne steht im Frühlingspunkt) betrug die mittlere Länge der Erde 180 Grad. Dann betrug sie am Anfang
des Jahres
| $$\begin{equation}
L_0 = 180^\circ - \frac{31+28+21}{365.25} 360^\circ \approx 100^\circ
\end{equation}$$ | (22) |
Berechnung der Bahnelemente
Wir haben nun alles notwendige um die Bahnelmente für z.B. die Venus zu einem konkreten Zeitpunkt zu berechnen.
Das folgende Javascript-Snippet erledigt die Berechnung:
// orbital elements
var planet = global.planet = calc.orbitalElements(data.venus, global.julianDate);
// orbital elements calculated direclty from JPL tables
print("semi major axis :", planet.semiMajorAxis);
print("eccentricity :", planet.eccentricity);
print("inclination :", math.formatAngle("degrees-simple",planet.inclination));
print("mean longitude :", math.formatAngle("degrees-simple",planet.meanLongitude));
print("longitude of perihelion :", math.formatAngle("degrees-simple",planet.longitudePerihelion));
print("longitude ascending node :", math.formatAngle("degrees-simple",planet.longitudeAscendingNode));
// derived orbital elements
print("argument perihelion :", math.formatAngle("degrees-simple",planet.argumentPerihelion));
print("mean anomaly :", math.formatAngle("degrees-simple",planet.meanAnomaly))
planet
ist eine Instanz der Klasse
OrbitalElements
. Die Klasse
OrbitalElements
berechnet
die Bahnelemente gemäß der JPL Daten, z.B. gemäß Formel
20 . Die Implementierung
der Klassen finden sie in Bibliothek
astro.calc.js
.
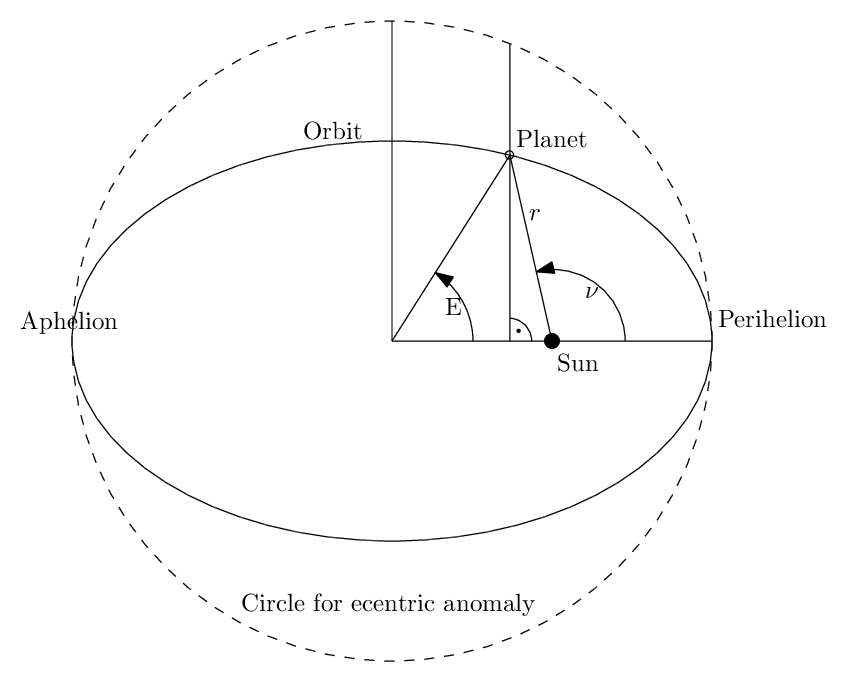
Planet: Exzentrische Anomalie
Keplergleichung
Zuerst müßen wir die Koordinaten des Planeten im Orbitalsystem (siehe Abschnitt
Orbitalsystem
) berechnen: Wir interessieren uns
für die wahre Anomalie
\(\nu\)and den Abstand
\(r\)von der Sonne.
Dazu müßen wir allerdings zuerst eine Zwischengröße die exzentrischen Anomalie
\(E\)berechnen.
Den Zusammenhang zwischen der exzentrischen Anomalie und er wahren Anomalie können sie aus
Abbildung
15 entnehmen.
Die exzentrische Anomalie kann aus der mittleren Anomalie über die Keplergleichung
| $$\begin{equation}
E -e \sin (E) = M
\end{equation}$$ | (23) |
ermittelt. Diese Gleichung kann man leider nicht so umformen, daß man E direkt aus
M berechnen kann. Stattdessen muß man ein Iterationsverfahren verwenden.
| $$\begin{equation}
E_{i+1} = E_i - \frac{M-E_i+e\sin E_i}{e\cos E_i - 1}
\end{equation}$$ | (24) |
Man startet mit
\(E_0 =M\)und führt die Iteration dann solange durch bis die gewünschte Genauigkeit
\(\left | E_{i+1} - E_i \right | < \epsilon\)erreicht ist.
Berechnung der exzentrischen Anomalie
Mit Hilfe des folgenden Snippets können Sie die exzentrische Anomalie berechnen.
var planet = global.planet;
planet.eccentricAnomaly = calc.eccentricAnomaly(planet.meanAnomaly, planet.eccentricity);
print("eccentric anomaly : ", planet.eccentricAnomaly);
Die Funktion
calc.eccentricAnomaly
stellt das Iterationsverfahren bereit.
Siehe hierzu die Bibliothek
astro.calc.js
.
calc.eccentricAnomaly = function (meanAnomaly, eccentricity) {
var eccentricAnomaly = meanAnomaly + eccentricity * Math.sin(meanAnomaly);
var deltaEccentricAnomaly = 1;
while (Math.abs(deltaEccentricAnomaly) > 0.0000001) {
deltaEccentricAnomaly = (meanAnomaly -
eccentricAnomaly + eccentricity * Math.sin(eccentricAnomaly)) /
(1 - eccentricity * Math.cos(eccentricAnomaly));
eccentricAnomaly += deltaEccentricAnomaly;
}
return eccentricAnomaly;
};
Planet: Orbitalsystemkoordinaten
Nun kennen wir die exzentrische Anomalie und können daraus die wahre Anomalie und den Abstand zur Sonne berechnen
| $$\begin{eqnarray}
r&=&a(1-e\cos E)\\
\tan \frac{\nu}{2} &=& \sqrt{\frac{1+e}{1-e}}\tan \frac{E}{2}
\end{eqnarray}$$ | (25) |
| (26) |
Die Umsetzung finden sie in Bibliothek
astro.calc.js
.
calc.orbitalCoordinates = function (semiMajorAxis, eccentricity, eccentricAnomaly) {
var lambda = 2 * Math.atan(Math.sqrt((1 + eccentricity) /
(1 - eccentricity)) * Math.tan(eccentricAnomaly / 2));
var rad = semiMajorAxis * (1 - eccentricity * Math.cos(eccentricAnomaly));
return {
lambda: lambda,
rad: rad
};
};
Das folgende Javascript-Snippet führt die Berechnung durch. Aus den Polarkoordinaten
\(\nu\)und
\(r\)wird dann
anschließend ein Vektorobjekt gebaut. Das Vektorobjekt benutzt intern kartesische Koordinaten.
In kartesischen Koordinaten sind Vektoradditionen, Subtraktionen oder eine Vektorrotationen sehr einfach.
Das Vektorobjekt stellt entpsrechende Methode zur Verfügung, welche im Folgenden nützlich sind.
// orbital coordinates
var planet = global.planet;
planet.orbitalCoordinates = calc.orbitalCoordinates(
planet.semiMajorAxis,
planet.eccentricity,
planet.eccentricAnomaly);
print("lambda : ", math.formatAngle("degrees-simple",planet.orbitalCoordinates.lambda));
print("radius : ", planet.orbitalCoordinates.rad);
// make vector from orbital coordinates
planet.orbitalPosition = math.vector(
0,
planet.orbitalCoordinates.lambda,
planet.orbitalCoordinates.rad, 'spherical');
print("orbital coordinates :", planet.orbitalPosition.format("spherical-degrees"));
Die Vektorklasse ist in Bibliothek
astro.math.js
definiert.
Planet: Heliozentrisch ekliptikale Koordinaten
Wir wollen nun die Koordinaten vom orbitalen Koordinatensystem in das heliozentrische Koordinatensystem umrechnen.
Das orbitale Koordinatensystem geht aus dem heliozentrischen durch die folgenden Drehungen hervor (siehe
18 ).
Drehung
- um den Winkel
\(\Omega\)um die Z-Achse drehen
- um den Winkel
\(i\)um die (neue) X-Achse drehen
- um den Winkle
\(\omega\)um die (neue) Z-Achse drehen
Wir benutzen nun Matrixschreibweise für die kartesischen Koordinaten des Planetenvektors
\(\vec{r}\). Einmal für
die orbitalen kartesischen Koordinaten
| $$
\mathbf{x}_{orbital} = \begin{pmatrix} x_{orbital} \\ y_{orbital} \\ z_{orbital}\end{pmatrix}
$$ |
Und auch für die heliozentrischen kartesischen Koordinaten
| $$
\mathbf{x}_{heliocentric} = \begin{pmatrix} x_{heliocentric} \\ y_{heliocentric} \\ z_{heliocentric}\end{pmatrix}
$$ |
Nun können wir durch Anwendung von Rotationsmatrizen zwischen den Koordinatensystem umrechnen:
| $$
\mathbf{x}_{heliocentric} = R_z(\Omega) R_x(i) R_z(\omega)\mathbf{x}_{orbital}
$$ |
|
bzw.
| $$
\mathbf{x}_{orbital} = R_z(-\omega) R_x(-i) R_z(-\Omega)\mathbf{x}_{heliocentric}
$$ |
Dabei sind
\(R_z(\alpha)\)und
\(R_x(\alpha)\)Rotationsmatrizen
| $$\begin{eqnarray}
R_z(\alpha) &=& \begin{pmatrix} \cos \alpha && -\sin \alpha && 0 \\
\sin \alpha && \cos \alpha && 0 \\
0 && 0 && 1
\end{pmatrix} \\
R_x(\alpha) &=& \begin{pmatrix} 1 && 0 && 0 \\
0 && \cos \alpha && -\sin \alpha \\
0 && \sin \alpha && \cos \alpha
\end{pmatrix}
\end{eqnarray}$$ | (27) |
| (28) |
Hier das Javascript Snippet um die Berechnung konkret durchzuführen:
var planet = global.planet;
planet.heliocentricEclipticPosition = planet.orbitalPosition
.rotZ(planet.argumentPerihelion)
.rotX(planet.inclination)
.rotZ(planet.longitudeAscendingNode);
print("heliocentric ecliptic coordinates :",
planet.heliocentricEclipticPosition.format("spherical-degrees"));
Wir benutzen hier die Rotationsmethoden des Vektorobjekts.
vector.rotX = function (alpha) {
var result = math.vector();
result.x = this.x;
result.y = Math.cos(alpha) * this.y - Math.sin(alpha) * this.z;
result.z = Math.sin(alpha) * this.y + Math.cos(alpha) * this.z;
return result;
}
Siehe hierzu die Bibliothek
astro.math.js
.
Erde: Bahnelemente
Im folgenden müßen wir die Berechnungen für die Erde wiederholen. Wir starten mit
den Bahnelementen der Erde.
// orbital elements
var earth = global.earth = calc.orbitalElements(data.earth, global.julianDate);
// orbital elements calculated directly from JPL tables
print("semi major axis :", earth.semiMajorAxis);
print("eccentricty :", earth.eccentricity);
print("inclination :", math.formatAngle("degrees-simple",earth.inclination));
print("mean longitude :", math.formatAngle("degrees-simple",earth.meanLongitude));
print("longitude of perihelion :", math.formatAngle("degrees-simple",earth.longitudePerihelion));
print("longitude ascending node :", math.formatAngle("degrees-simple",earth.longitudeAscendingNode));
// derived orbital elements
print("argument perihelion :", math.formatAngle("degrees-simple",earth.argumentPerihelion));
print("mean anomaly :", math.formatAngle("degrees-simple",earth.meanAnomaly))
Erde: Exzentrische Anomalie
Durch Lösung der Keplergleichung bestimmen wir aus der mittleren Anomalie die exzentrische Anomalie der Erde.
var earth = global.earth;
earth.eccentricAnomaly = calc.eccentricAnomaly(earth.meanAnomaly, earth.eccentricity);
print("eccentric anomaly : ", earth.eccentricAnomaly);
Erde: Orbitalsystemkoordinaten
Aus der exzentrischen Anomalie können wir nun die wahre Anomalie der Erde berechnen.
// orbital position
var earth = global.earth;
earth.orbitalCoordinates = calc.orbitalCoordinates(earth.semiMajorAxis,
earth.eccentricity,
earth.eccentricAnomaly);
print("lambda : ", math.formatAngle("degrees-simple",earth.orbitalCoordinates.lambda));
print("radius : ", earth.orbitalCoordinates.rad);
// make vector from orbital coordinates
earth.orbitalPosition = math.vector(0,
earth.orbitalCoordinates.lambda,
earth.orbitalCoordinates.rad, 'spherical');
print("orbital coordinates :", earth.orbitalPosition.format("spherical-degrees"));
Erde: Heliozentrisch ekliptikale Koordinaten
Als nächste bestimmen wir die heliozentrischen Koordinaten der Erde
indem wir durch Anwendung von Rotationsmatrizen zwischen den
Koordinatensystemen umrechnen.
var earth = global.earth;
earth.heliocentricEclipticPosition = earth.orbitalPosition
.rotZ(earth.argumentPerihelion)
.rotX(earth.inclination)
.rotZ(earth.longitudeAscendingNode);
print("heliocentric ecliptic coordinates :",
earth.heliocentricEclipticPosition.format("spherical-degrees"));
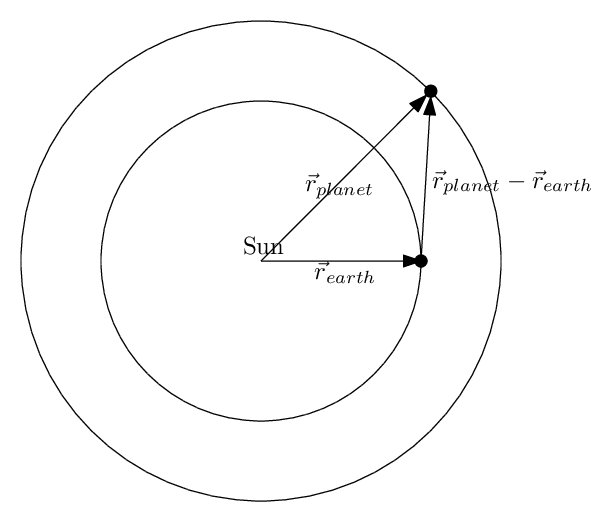
Planet: Geozentrisch ekliptikale Koordinaten
Aus den heliozentrisch ekliptikalen Koordinaten des Planeten und der Erde können
wir nun die geozentrisch ekliptikalen Koordinaten des Planeten berechnen.
Das geozentrisch ekliptikalen Koordinatensystem erhält man indem man
den Ursprung des heliozentrisch eklipitikalen Koordinatensystems ins Zentrum der Erde verschiebt.
Wir können also durch einfache Vektorsubktration die kartesichen Koordinaten eines
Planeten zwischen dem heliozentrischen und dem geozentrischen Koordinatensystem umrechnen
| $$
\mathbf{x}_{planet,geocentric} = \mathbf{x}_{planet,heliocentric} - \mathbf{x}_{earth,heliocentric}
$$ |
Hier das Javascript Snippet, welches die Vektorsubtraktion durchführt.
var planet = global.planet;
var earth = global.earth;
planet.geocentricEclipticPosition = planet.heliocentricEclipticPosition
.subtract(earth.heliocentricEclipticPosition);
print("geocentric eclpitic coordinates :",
planet.geocentricEclipticPosition.format('spherical-degrees'));
Planet: Geozentrisch äquatoriale Koordinaten
Als letzten Schritt rechnen wir dir geozentrisch eklipitikalen Koordinaten noch
in das geozentrisch äquatoriale System um. Hierzu genügt es eine Rotationsmatrix
auf die kartesischen Koordinaten anzuwenden.
| $$
\mathbf{x}_{planet, equatorial} = R_x(\epsilon) \mathbf{x}_{planet,geocentric}
$$ |
Hier bei ist
\(\epsilon\)der Winkel zwischen Erdäquatoreben und Ekliptikalebene.
Hier das Javascript Snippet um die Berechnung durchzuführen
var planet = global.planet;
planet.geocentricEquatorialPosition = planet.geocentricEclipticPosition
.rotX(calc.eclipticAngle(global.julianDate));
print("geocentric equatorial coordinates :",
planet.geocentricEquatorialPosition.format('spherical-hours'));
Sternkarte
Und ganz zum Schluss können wir unsere Planetenposition noch in eine Sternkarte eintragen.
var planet = global.planet;
// create map
var mymap = map.simpleMap({
paper : raphael(document.getElementById("calckeplermap"), 500, 500)
});
// add planet
planet.color="red";
planet.title="Planet";
mymap.addPlanet(planet.geocentricEquatorialPosition);
// draw map
mymap.draw();
Vergleich Kreisbahn mit Ellipsenbahn
Hier ein Vergleich: Die Planetenposition wurde einmal mittels
der Kreisbahnnäherung berechnet und ein zweites Mal mit
unter Annahme einer elliptischen Bahn:
Sternkarte
.